BucketList<T>
March 21, 2021TL;DR:
BucketList<T>is a data structure that performs exceptionally well for a certain usage scenario:
n(list size) is large.- Fast index-based access:
list.GetItemAt(i).- Fast index-based removal:
list.RemoveAt(i).In my use case, this reduced the runtime from 7 hours to 17 seconds!
An Interesting Problem
In December of last year I took part in solving the Advent of Code programming puzzles for the first time. Since then I became a bit obsessed with that and started solving also the older events going back until 2015.
Day 19 of 2016 presented an interesting challenge
that took me a while to solve (with a reasonable runtime) and led to the solution based
on this BucketList<T> data structure.
The basic idea behind this problem is that we have a:
- Circular data structure.
- Maintain a current element.
- Find the element opposite of the current element.
- Advance the current element by one.
- Repeat until the list has only one element left.
A poor solution
My first approach was using a LinkedList which performed OK for small list sizes.
But for large lists (e.g. 3.001.330 was my puzzle input) the performance was dismal.
List size: 3001330.
END after 26696.1142087 seconds.
That's a runtime of more than 7 hours 😬.
The problem was the linear search for locating the opposite element in the list that caused
an O(n²) complexity.
Using a simple List<T> (instead of LinkedList<T>) performed equally bad because
in that case the remove operation causes a runtime complexity of O(n²).
To sum it up:
| Data Structure | Lookup | Removal |
|---|---|---|
List<T> |
O(1) |
O(N²) |
LinkedList<T> |
O(N²) |
O(1) |
A better (by a lot) solution
So I needed a data structure with linear or better performance for:
- Indexing
- Removal
My solution was a custom data structure I called BucketList (ha ha) which:
- maintains the elements in a list of lists
- that have the same maximum size (hence, buckets).
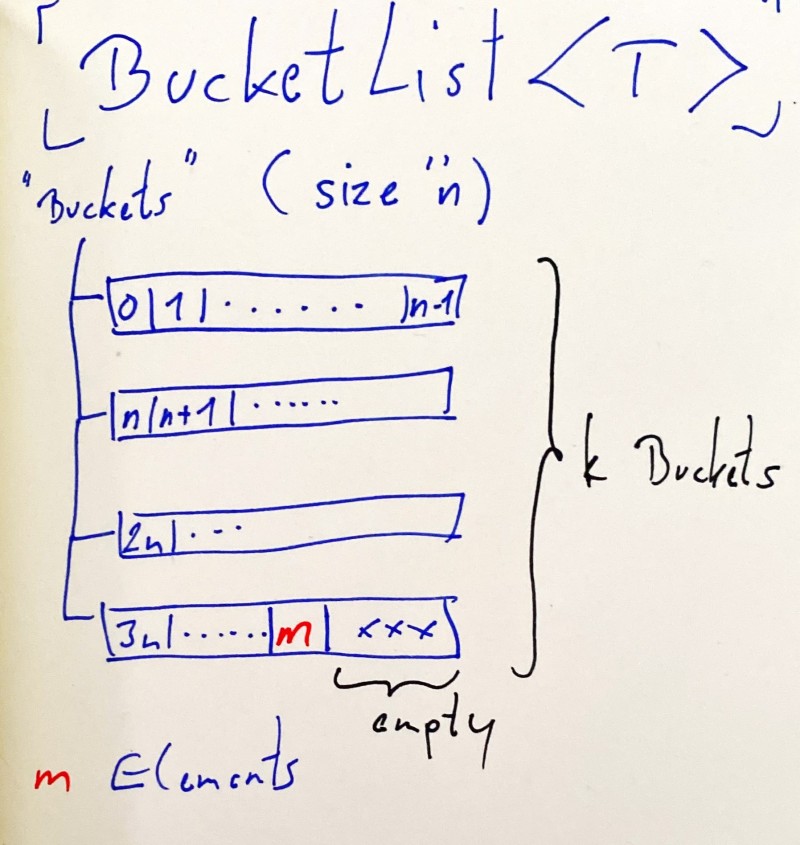
This way, when performing an index-based lookup I have nearly constant¹ O(1) access to elements
and removal is only limited by the List<T> performance of a single bucket.
¹ Actually O(k) where k amounts to the number of buckets which should be negligibly low compared
to n.
To sum it up:
| Data Structure | Lookup | Remove |
|---|---|---|
BucketList<T> |
O(k) |
O(n) |
k: number of buckets
n: bucket size (list size N / k)
This brought the runtime down dramatically!
List size: 3001330.
END after 17.0722168 seconds.
17 seconds ... way better 🤩.
Here's the full source code for BucketList.
Note: A bucket size of
25.000worked best in that specific scenario but your mileage may vary, of course, and depends on the problem input size.
Caveats
- I only used
BucketList<T>for this specific problem so far. - The runtime performance depends on the selection of a bucket size for a given list size.
- The
InsertAtcase is not yet considered. - I'm sure that this data structure exists already with a different name. However, I came up with this on my own when solving my problem, so give me that ;-).